評価実験の内容をエクセルで集計し、グラフ化する一般的な流れを示します。
＊エクセルでの数値の算出等のサンプルファイルを以下から取得してください。
　Common / 配布 / プロトタイプシミュレーション（柿山）/ 13/ sample_data.xls

●平均値（=AVERAGE(範囲)）
　回答者の回答の平均値

●標準偏差（=STDEV(範囲)）
　回答者の回答のバラツキ度合い

　　→　平均値と標準偏差を総合的にみて考察すること

＊標準偏差グラフのY誤差範囲の表示方法
　・まず、平均値をグラフ化する【平均値の値群を選択／グラフ／散布図】
　・散布図のプロットされた任意の点を右クリックし【データ系列の書式設定】を選択
　・【誤差範囲／Y誤差範囲／ユーザー設定／値の指定／】
　・正の誤差の値、負の誤差の値、いずれも標準偏差の値群を選択

グラフをもとに、提案したデザイン提案に対する評価結果に対する考察を行う一般的な流れをしめします。また、この考察は、改善案を創出する為のものとなります。

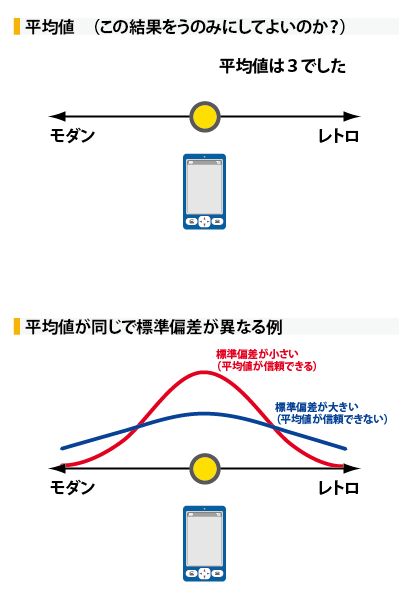
●平均値と標準偏差による考察の考え方
　平均値だけを単純にみてはいけません。標準偏差（データのバラツキ度合い）をみて、バラツキ具合が少なければ、平均値を信用し、考察します。バラツキ度合いが大きければ、平均値を信頼してはいけないことになります。何故バラツイタのか考察しましょう。

　　　　　　

●（今回は被験者数が少ないので難しいですが）被験者のパーソナリティーの違いに着目した考察もできるとベターです（男女の違い、年齢の違い、経験の違い等）。

　　　　　　

 

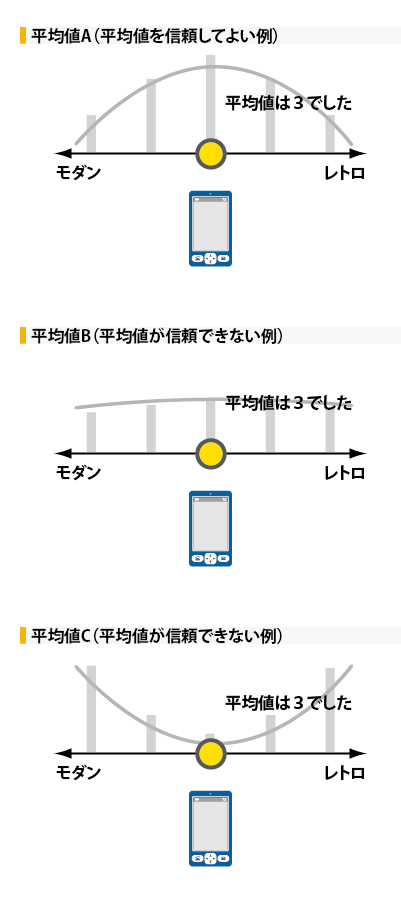
散布図の重要性

＊散布図グラフ描画と相関係数の表示方法
　・まず、比較したい２つの変数を選ぶ
（Macの場合commandボタンを押しながら２回に分けて、エクセルの数値を選択する）

　・その後【グラフ／散布図】で散布図を描く
　・データの取得方法によっては一つの点に、複数の点が重なることがある...。
　・散布図のプロットされた任意の点を右クリックし【近似曲線の追加】を選択
　・【オプション／グラフにR-2乗値を表示する】を選択してOK

　　　　　　　

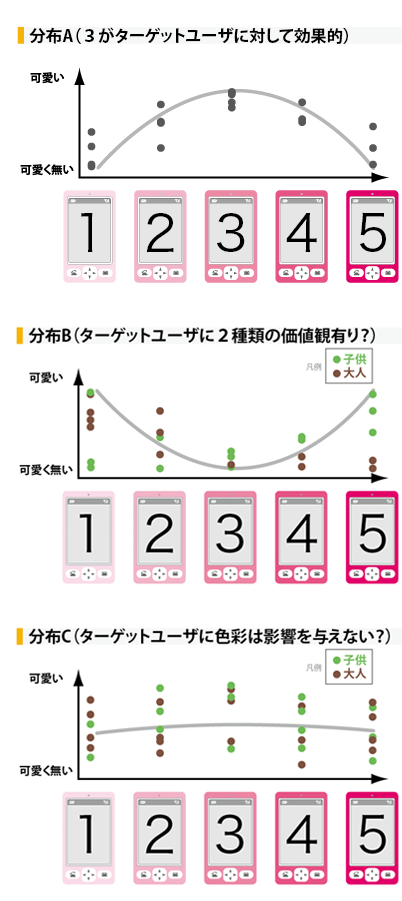
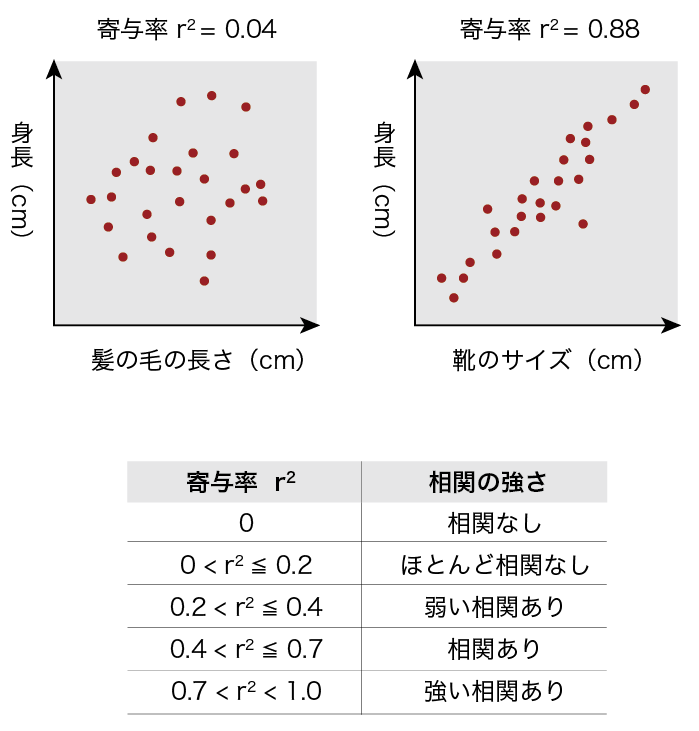
相関関係と寄与率（r2）

　対になった２つのデータ群（ex.XとY）の相関関係で
　自らのデザインに有用な法則を見いだすのが目的です。
　「ex. 角が丸くなるほど、カワイイ印象になる」
　「メタボの自覚がある人ほど、提案を高く評価する」

 

１. インスペクション（査察）法　【開発者自身の評価】
　・ヒューリスティック法　「インタラクションデザインにて解説済み」
　・認知的ウォークスルー法　「インタラクションデザインにて解説済み」

２. ユーザテスト法　【被験者を対象にした評価】
　・主観評価（SD法）　「インタラクションデザインにて経験済み」
　・プロトコル解析　「インタラクションデザインにて経験済み」
　・パフォーマンステスト （実際に数字で表れる評価・成績評価）

提出物の仕様：
　１.本日の内容を元にした（場合によってはアンケートのやり直し？）データの分析
　２.分析結果に基づく考察
　３.考察に基づく改善案の提案